상세 컨텐츠
본문
여러 가지 확률 분포 (1)
통계를 실무적으로 쓸 때 중요한 모집단, 표본, 추출을 정의해보고 여러 가지 확률 분포에 대해 공부하고자 한다.
모집단과 표본
통계 조사에서는 어떤 관심의 대상인 모집단으로부터 n개를 랜덤으로 골라서 조사한 후, 전체, 즉 모집단에 대해 추측한다. 이 때 조사와 추측의 대상이 되는 전체를 모집단(population)이라고 하고, 전체가 어떻게 흩어져 있는지 묘사하는 분포를 모집단 분포(population distribution)이라고 한다.
N개의 개체로 구성된 모집단에서 '랜덤'하게 n개를 택한다는 것은 순차적으로 한 개씩 동일한 확률로 뽑아가고 한 번 뽑은 것은 다시 돌려 넣지 않는 비복원추출(sampling without replacement)을 의미한다. 이러한 추출방법을 단순랜덤추출(simple random sampling)이라 한다.

이렇게 추출된 n개의 개체를 랜덤표본(random sample) 또는 간단하게 표본(sample)이라고 한다.
이항분포와 관련된 분포들
여러 가지 확률 분포들 중 많은 분포들이 이항분포와 관련되어 있다.
1. 베르누이 분포 (Bernoulli distribution)
어떤 실험을 했을 때 임의의 결과가 '성공'과 '실패'의 두 가지 중 하나로 나오는 실험(또는 시행)을 베르누이 시행(Bernoulli experiment or trial)이라고 한다. 시행을 여러 번 할 때, '성공'의 횟수를 X, '성공'의 확률을 p라고 하자.
- 기호:

- 특성들:
- (밀도함수, 정의)

- (적률생성함수)

- (평균과 분산)

- (밀도함수, 정의)
- 증명:

(참고)
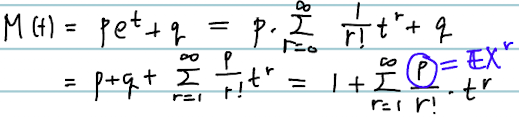
이항전개
이항분포를 다루기 전에 이항전개에 대해 알아보자.
이항 계수(binomial coefficient)의 정의:

(참고) 내림 팩토리얼(descending factorial)과 오름 팩토리얼(ascending factorial)
- 내림 팩토리얼:

- 오름 팩토리얼:

이항전개의 성질들
(1)

(2)

(3)

(4)

(5)

2. 이항분포 (Bonomial distribution)
모집단을 구성하고 있는 각 개체의 특성이 '0' 또는 '1'의 두 가지로 분류되어 있고 '1'의 비율이 p일 때, 모집단에서 한 개씩 동일한 확률로 뽑아 나가며 복원추출(sampling with replacement)을 하는 경우, 뽑은 n개 중에서 '1'의 개수를 X라고 가정하자.
베르누이 과정(Bernoulli process)

일 때, 확률 변수들의 모임 $(X_n)_{n\leq1}$ 베르누이 과정이라 한다.
- 기호:

- 특성들:
- (밀도함수, 정의)

- (적률생성함수)

- (평균과 분산)

- (베르누이 분포의 합)

- (밀도함수, 정의)
<김우철> 수리통계학 및 서울대학교 수리통계 1 강의 내용을 바탕으로 작성함.
'Research' 카테고리의 다른 글
| Git 사용법 (3) (0) | 2024.04.25 |
|---|---|
| Git 사용법 (2) (0) | 2024.04.25 |
| Git & Github 사용법 (1) (0) | 2024.04.25 |
| "xcrun: error: invalid active developer path"오류 (0) | 2024.04.25 |




